数学初二上 第十九章 几何证明
19.8 直角三角形的性质（1）
1、选择题
1．如图，在Rt△ABC中，∠ACB=90°，BC的垂直平分线交斜边AB于D，AB=12 cm，AC=6 cm，则图中等于60°的角共有 （ ）
A．2个 B．3个 C．4个 D．5个
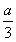
第1题 第2题 第3题 第8题 第9题
2. 如图，Rt△ABC中，∠B=90°，∠ACB=60°，延长BC到D，使CD=AC则AC：BD= （ ）
A．1：2 B．1：3 C．2：3 D．3:4
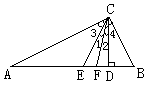
3. 如图，在Rt△ABC中，∠ACB=90°，CD、CE，分别是斜边AB上的高与中线，CF是∠ACB的平分线.则∠1与∠2的关系是 （ ）
A．∠1<∠2 B．∠1=∠2; C．∠1>∠2 D．不可以确定
4. 在直角三角形ABC中，若∠C=90°，D是BC边上的一点，且AD=2CD，则∠ADB的度数是 （ ）
A．30° B．60° C．120° D．150°
5、在△ABC中, ∠A: ∠B: ∠C=1:2:3,CD⊥AB于D,AB=
,则DB等于
A.
B. C. 
D. 
6下列命题错误的是 （ ）
A．有两个角互余的三角形肯定是直角三角形；
B．三角形中，若一边等于另一边一半，则较小边对角为30°
C．直角三角形斜边上的中线等于斜边的一半；
D．△ABC中，若∠A：∠B：∠C=1：4：5，则这个三角形为直角三角形。
7、假如三角形的两条边上的垂直平分线的交点在第三条边上，那样这个三角形是
A.锐角三角形 B.等腰三角形 C.直角三角形 D.钝角三角形
8、将一张长方形纸片ABCD如图所示折叠，使顶点C落在C′点. 已知AB=2,∠DEC′=30°,则折痕DE的长为 （ ）
A 、4 B、
C、2 D、1
9、如图，∠BCA=90，CD⊥AB，则图中与∠A互余的角有 （ ）
A．1个 B、2个 C、3个 D、4个
10. 具备下列条件的△ABC中，不是直角三角形的是 （ ）
A．∠A-∠B=∠C B、∠A=3∠C，∠B=2∠C
C、∠A=∠B=
∠C D、∠A=∠B=2∠C
2、填空题
11、“直角三角形两锐角互余”__________逆定律
12、直角三角形中一个锐角为30°,斜边和最小的边的和为12cm,则斜边长为 __________.
13、等腰直角三角形的斜边长为3,则它的面积为__________ .
14、等腰三角形一腰上的高等于该三角形一条边长度的一半,则其顶角为__________.
15、已知在△ABC中，∠ACB=90°，CD是高，∠A=30°，AB=4cm,则BC=_______cm,∠BCD=_______，BD=_______cm，AD=________cm；
16、已知三角形的的三个内角的度数之比为1：2：3，且最短边是3厘米，则最长边上的中线等于____________；
17、在△ABC中，∠C=90°，∠A、∠B的平分线相交于O，则∠AOB=_________；
18、等边三角形的高为2，则它的面积是__________。
19、在直角△ABC中，∠C=90°，∠BAC=30°，BC=10，则AB=________.
20．在直角△ABC中，∠ACB=90°，CD是AB边上中线，若CD=5cm,则AB=__________。
21.. 在直角三角形ABC中，∠ACB=90°，CD是AB边上中线，图中有__________等腰三角形.
顶角为30°的等腰三角形，若腰长为2，则腰上的高__________，三角形面积是________
等腰三角形顶角为120°，底边上的高为3，则腰长为_________
△ABC中，AB=AC=6，∠B=30°，则BC边上的高AD=_______________
25、在RtΔABC中，∠A=30°则∠C=90°，CD是斜边的中线，则图中的等腰三角形是____________________，等边三角形是__________.
26、 在RtΔABC中，斜边长为6cm，则斜边上的中线为____________________ cm.
27、在Rt△ABC中,∠C=90度,∠B=15度,则∠A=______度
28、在Rt△ABC中，∠C=90º，∠A=30º，AB=10cm，则BC=_____cm。
29. 如图，在△ABC中，∠B=30°，ED垂直平分BC，ED=3．则CE长为____________________．
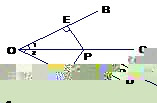
第29题 第30题 第31题 第32题
30、如图，在△ABC中，AB=AC =10，CE=4，MN是AB的垂直平分线， BE =__________
31、如图，已知Rt△ABC中，∠BAC=90º ，AD是上的中线,AB=12,AC=5，那样AD = __________
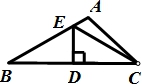
32、如图：OC是∠AOB=60º的平分线，点P是OC上的一点，PD⊥OA，PE⊥OB，垂足分别为点D、E，若PD+PE=6，则OP=__________ .
33. “直角三角形斜边上的中线等于斜边的一半”的逆命题是__________
__________。
3、解答卷
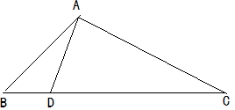
34、如图,已知∠BAC=90°,∠C=30°,AD⊥BC于D,DE⊥AB于E,BE=3,求BC的长 .
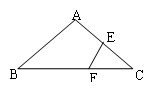
35、如图,已知在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.求证:BF=2CF.
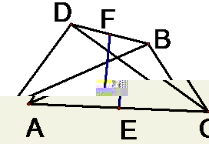
36、小明站在高为30米的楼上C处,测得一条河边一点A的俯角为30°,河对岸一点B的俯角为15°,问河宽约多少米?
37、在△ABC中，∠BAC=90°，DE=8cm，AD是高，AE是斜边上的中线，且DC=AC，求∠B 的度数及AE的长。
38、如图，在矩形ABCD中，AB=12，BC=6，将矩形沿对角线AC折迭，点D落在点D′处，求重迭部分△AEC的面积．
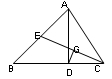
39、如图，△ABC中，AD是高，CE是中线，DC＝BE，DG⊥CE于G。
（1）求证：G是CE的中点；
（2）∠B＝2∠BCE。
40. 已知：四边形ABCD中，∠ABC= ∠ADC=90º，E、F分别是AC、BD的中点。
求证：EF⊥BD
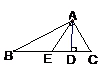
如图，在△ABC中，∠B= 2∠C，点D在 BC 边上，且AD ⊥AC. 求证：CD=2AB
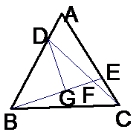
42、在等边三角形ABC中，点D、EF分别在AB、AC边上，AD=CE，CD与BE交与F，DG ⊥BE。
求证：（1）BE=CD; DF=2GF
数学初二上 第十九章 几何证明
19.8 直角三角形的性质（1）
参考答案
1、 选择题
1. D
2. C 设BC=x则AC=2x，CD=2x ∴BD=3x∴AC：BD=2：3
3. B
∵CE为△ABC中线,∴AE=EC
∴∠3=∠A
∵CF平分∠ACB
∴∠ACF=∠FCB 即∠3+∠1=∠2+∠4
∵CD⊥AB，∠ACB=90°∴∠4=∠A
∴∠3+∠1=∠2+∠A
∴∠1=∠2
4. C ∠ADC=60°∴∠ADB=120°
5. C
6. B
7. C
8．A
9. B
10. D
2、 填空题
11.有
12 8cm
13. 
14. 30°或120°
15. 2 30° 1 3
16. 3cm
17.135°
18.
19. 20
20. 10cm
21. 2个
22. 1 1
23. 6
24. 3
25. ΔACD和ΔBCD ΔBCD
26. 3
27. 75
28. 5
29. 6
30. 6
31. 
32. 6
33. 假如三角形一边上的中线等于这条边的一半，那样这个三角形是直角三角形．
3、 解答卷
34. BC的长为24.
35、提示：联结AF.
36、河宽约60米。
37、∠B的度数为30º, AE的长为16cm。
38、重迭部分△AEC的面积为
．
提示：记AB与CD’的交点为E，证明△AD’E≌△CBE，Rt△AD’E中，
由
得
39、提示：联结DE。 （1）证明略 （2）证明略
40. 提示：联结BE、DE
41. 提示：取CD的中点E，联结AE
42. （1）提示：证△BCE≌△CAD
（2）提示：∵△BCE≌△CAD ∴∠CBE=∠ACD ∵∠DFG=∠CBE+∠BCF ∴∠DFG=∠BCD+∠ACD=60°
